LIMITES

Antes de arrancar el calculo pre uni, si no has entendido bien
como se interpreta limites con la definicion formal, no entenderas
las posteriores demostraciones cuando usen delta y epsilon.
Este libro con sus pocas paginas te prepara bien para entender todo sobre
limites.

Calculo diferencial

Libro ideal para arrancar con calculo pre uni
Con este aprendì derivadas y su interpretacion geometrica.

Calculo Vectorial

El final del camino de todo el calculo avanzado, en varias unis
le dicen creo que calculo 3, terminado esto, puedes adentrarte a las entrañas
del algebra lineal y el algebra abstracta.
Aunque no es obligatorio ese orden.
Bien se pueden estudiar en paralelo.

\[\int k \, dx = kx + C\] \[\int x^n \, dx = \frac{x^{n+1}}{n+1} + C \quad (n \neq -1)\] \[\int \frac{1}{x} \, dx = \ln |x| + C\] \[\int e^x \, dx = e^x + C\] \[\int a^x \, dx = \frac{a^x}{\ln a} + C \quad (a>0, a \neq 1)\] \[\int \sin x \, dx = -\cos x + C\] \[\int \cos x \, dx = \sin x + C\] \[\int \sec^2 x \, dx = \tan x + C\] \[\int \csc^2 x \, dx = -\cot x + C\] \[\int \sec x \tan x \, dx = \sec x + C\] \[\int \csc x \cot x \, dx = -\csc x + C\] \[\int \frac{1}{\sqrt{1-x^2}} \, dx = \arcsin x + C\] \[\int \frac{-1}{\sqrt{1-x^2}} \, dx = \arccos x + C\] \[\int \frac{1}{1+x^2} \, dx = \arctan x + C\] \[\int \frac{-1}{1+x^2} \, dx = \text{arccot}\, x + C\] \[\int \frac{1}{x\sqrt{x^2-1}} \, dx = \arcsec x + C\] \[\int \frac{-1}{x\sqrt{x^2-1}} \, dx = \arccsc x + C\]

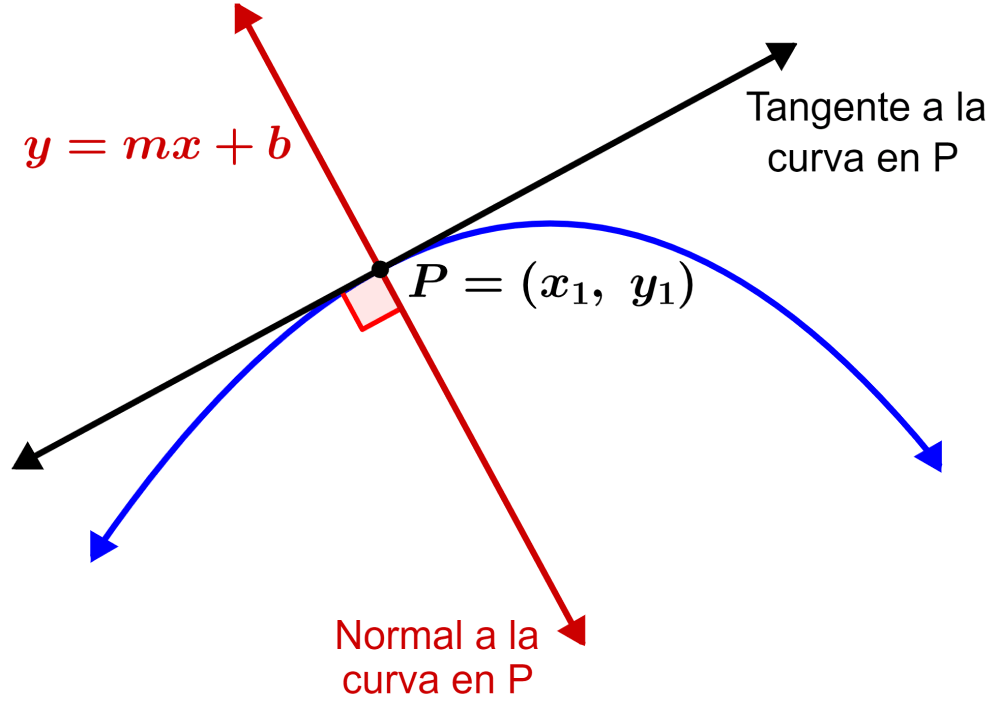
La pendiente de una recta tangente se define como \[m = \tan(\alpha)\] Cuando \(\alpha \to 0\), se cumple que \[m = \tan(\alpha) = \frac{\Delta y}{\Delta x}\] Es decir, la pendiente es el cociente entre el incremento en \(y\) y el incremento en \(x\). De esta manera se obtiene la ecuación de la recta tangente en un punto \((x_0, y_0)\): \[y - y_0 = m(x - x_0)\] Recta tangente: \[\quad y - y_0 = f'(x_0)\,(x - x_0)\] Recta normal: \[\quad y - y_0 = -\frac{1}{f'(x_0)}\,(x - x_0)\]

INYECTIVIDAD

1). Primer ejemplo de inyectividad.

2). Segundo ejemplo de inyectividad.

SOBREYECTIVIDAD

1).Primer ejemplo de sobreyectividad.

2).Segundo ejemplo de sobreyectividad.

BIYECTIVIDAD

1).Primer ejemplo de biyectividad.

2).Segundo ejemplo de biyectividad.

Las derivadas de funciones trigonométricas surgen aplicando reglas primarias + la regla de la cadena. Primero se obtienen las formas simples (sin x, cos x, tan x) y después se generalizan a funciones compuestas (sin(f(x)), cos(f(x)), ...).

1. Seno de x: \[\quad \frac{d}{dx}\big(\sin x\big) = \cos x\] 2. Seno de una función: \[\quad \frac{d}{dx}\big(\sin(f(x))\big) = \cos(f(x)) \cdot f'(x)\] 3. Coseno de x: \[\quad \frac{d}{dx}\big(\cos x\big) = -\sin x\] 4. Coseno de una función: \[\quad \frac{d}{dx}\big(\cos(f(x))\big) = -\sin(f(x)) \cdot f'(x)\] 5. Tangente de x: \[\quad \frac{d}{dx}\big(\tan x\big) = \sec^2 x\] 6. Tangente de una función: \[\quad \frac{d}{dx}\big(\tan(f(x))\big) = \sec^2(f(x)) \cdot f'(x)\] 7. Cotangente de x: \[\quad \frac{d}{dx}\big(\cot x\big) = -\csc^2 x\] 8. Cotangente de una función: \[\quad \frac{d}{dx}\big(\cot(f(x))\big) = -\csc^2(f(x)) \cdot f'(x)\] 9. Secante de x: \[\quad \frac{d}{dx}\big(\sec x\big) = \sec x \cdot \tan x\] 10. Secante de una función: \[\quad \frac{d}{dx}\big(\sec(f(x))\big) = \sec(f(x)) \cdot \tan(f(x)) \cdot f'(x)\] 11. Cosecante de x: \[\quad \frac{d}{dx}\big(\csc x\big) = -\csc x \cdot \cot x\] 12. Cosecante de una función: \[\quad \frac{d}{dx}\big(\csc(f(x))\big) = -\csc(f(x)) \cdot \cot(f(x)) \cdot f'(x)\]

El concepto de límite en cálculo describe el valor al que se aproxima una función cuando la variable independiente se acerca a un punto. En trigonometría, hay dos límites fundamentales: 1) \[\lim_{\alpha \to 0} \frac{\sin \alpha}{\alpha} = 1\] Este límite es esencial porque permite definir la derivada de sin 𝑥 en 𝑥 = 0. 2) \[\lim_{h \to 0} \frac{\cos h - 1}{h} = 0\] Este aparece al calcular la derivada de cos x en x = 0. Ambos son la base para demostrar derivadas de funcions primarias y trigonometricas cuando su comportamiento se acerca a 0. Las derivadas primarias son reglas fundamentales que permiten calcular la derivada de funciones más complejas a partir de expresiones simples. Son la base del cálculo diferencial y se aplican en combinación para derivar prácticamente cualquier función. 1. Derivada de una constante: \[\quad \frac{d}{dx}(c) = 0\] 2. Derivada de una variable: \[\quad \frac{d}{dx}(x) = 1\] 3. Derivada de suma y diferencia: \[\quad \frac{d}{dx}(u + v - w) = \frac{du}{dx} + \frac{dv}{dx} - \frac{dw}{dx}\] 4. Derivada por una constante por función: \[\quad \frac{d}{dx}(c \cdot v) = c \cdot \frac{dv}{dx}\] 5. Derivada por una potencia: \[\quad \frac{d}{dx}(u^n) = n \, u^{\,n-1} \cdot \frac{du}{dx}\] 6. Derivada por un producto: \[\quad \frac{d}{dx}(uv) = u \cdot \frac{dv}{dx} + v \cdot \frac{du}{dx}\] 7. Derivada por un cociente: \[\quad \frac{d}{dx}\!\left(\frac{u}{v}\right) = \frac{v \cdot \frac{du}{dx} - u \cdot \frac{dv}{dx}}{v^2}\] 8. Derivada por cociente con constante: \[\quad \frac{d}{dx}\!\left(\frac{u}{c}\right) = \frac{1}{c} \cdot \frac{du}{dx}\] 9. Derivada Raiz cuadrada de una función: \[\quad \frac{d}{dx}(\sqrt{u}) = \frac{1}{2\sqrt{u}} \cdot \frac{du}{dx}\] 10. Derivada de raiz cuadrada de x: \[\quad \frac{d}{dx}(\sqrt{x}) = \frac{1}{2\sqrt{x}}\] 11. Regla de cadena: \[\quad \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}\]

\(\text{Función: } y = \arcsin(x)\) \(\text{Rama principal: } -\tfrac{\pi}{2} \leq y \leq \tfrac{\pi}{2}\)|\(-90^\circ \leq y \leq 90^\circ\)
\(\text{Función: } y = \arccos(x)\) \(\text{Rama principal: } 0 \leq y \leq \pi\)| \(0^\circ \leq y \leq 180^\circ\)
\(\text{Función: } y = \arctan(x)\) \(\text{Rama principal: } -\tfrac{\pi}{2} < y < \tfrac{\pi}{2}\)| \(-90^\circ < y < 90^\circ\)
\(\text{Función: } y = \arccot(x)\) \(\text{Rama principal: } 0 < y < \pi\)| \(0^\circ < y < 180^\circ\)
\(\text{Función: } y = \arcsec(x)\) \(\text{Rama principal: } 0 \leq y < \tfrac{\pi}{2} \;\; \cup \;\; \tfrac{\pi}{2} < y \leq \pi\)| \(0^\circ \leq y < 90^\circ \;\; \cup \;\; 90^\circ < y \leq 180^\circ\)
\(\text{Función: } y = \arccsc(x)\) \(\text{Rama principal: } -\tfrac{\pi}{2} \leq y < 0 \;\; \cup \;\; 0 < y \leq \tfrac{\pi}{2}\)| \(-90^\circ \leq y < 0^\circ \;\; \cup \;\; 0^\circ < y \leq 90^\circ\)

Las funciones recíprocas en trigonometría son pares de funciones que multiplicadas siempre dan 1, porque una es la inversa de la otra: \[ \sin A \cdot \csc A = 1 \qquad \Longrightarrow \qquad \csc A = \frac{1}{\sin A}, \quad \sin A = \frac{1}{\csc A} \] \[ \cos A \cdot \sec A = 1 \qquad \Longrightarrow \qquad \sec A = \frac{1}{\cos A}, \quad \cos A = \frac{1}{\sec A} \] \[ \tan A \cdot \cot A = 1 \qquad \Longrightarrow \qquad \cot A = \frac{1}{\tan A}, \quad \tan A = \frac{1}{\cot A} \]

Las identidades de ángulos complementarios relacionan funciones trigonométricas de un ángulo con las de su complemento \((90^\circ - A)\): \[\sin A = \cos\!\left(90^\circ - A\right) = \cos\!\left(\tfrac{\pi}{2} - A\right)\] \[\cos A = \sin\!\left(90^\circ - A\right) = \sin\!\left(\tfrac{\pi}{2} - A\right)\] \[\tan A = \cot\!\left(90^\circ - A\right) = \cot\!\left(\tfrac{\pi}{2} - A\right)\] \[\cot A = \tan\!\left(90^\circ - A\right) = \tan\!\left(\tfrac{\pi}{2} - A\right)\] \[\sec A = \csc\!\left(90^\circ - A\right) = \csc\!\left(\tfrac{\pi}{2} - A\right)\] \[\csc A = \sec\!\left(90^\circ - A\right) = \sec\!\left(\tfrac{\pi}{2} - A\right)\]

Función inversa de \(y=\sin(x)\) -> \(x=\arcsin(y)\).
Si se considera el arco tangente: \(x=\arcsin(y)\).
A veces \(y=\arcsin(x)\) es igual a \(y=\sin^{-1}(x)\).
El valor de seno esta definidio para cualquier valor de x en que \(-1 \leq x \leq 1\).

DERIVADAS DE LAS FUNCIONES INVERSAS

Las funciones logarítmicas tienen derivadas que dependen de la \textbf{regla de la cadena} y de la base del logaritmo. \[\text{Caso especial:} \quad \frac{d}{dx}(\ln x) = \frac{1}{x}, \quad x > 0\] \[\text{Para logaritmos en base } a: \quad \frac{d}{dx}(\log_a x) = \frac{1}{x \ln a}, \quad a > 0, \; a \neq 1\] Estas son la base de todas las demás fórmulas.

El breve repaso de los logaritmos nos dan las bases que consecuan a sus siguientes derivadas: \[\textbf{1.} \quad \log_a(1) = 0\] \[\textbf{2.} \quad \log_a(a) = 1\] \[\textbf{3.} \quad \log_a(a^x) = x\] \[\textbf{4.} \quad a^{\log_a x} = x\] \[\textbf{5.} \quad \log_a(xy) = \log_a x + \log_a y\] \[\textbf{6.} \quad \log_a\!\left(\frac{x}{y}\right) = \log_a x - \log_a y\] \[\textbf{7.} \quad \log_a(x^n) = n \cdot \log_a x\] \[\textbf{8.} \quad \log_a\!\left(\sqrt[n]{x}\right) = \frac{1}{n} \log_a x\] \[\textbf{9.} \quad \log_{a^n}(x) = \frac{1}{n} \log_a x\] \[\textbf{10.} \quad \log_a x = \frac{\ln x}{\ln a}\] \[\textbf{11.} \quad \log_a b = \frac{1}{\log_b a}\]

Un máximo relativo ocurre en un punto donde la función alcanza un valor mayor que en sus alrededores, y un minimo relativo donde la función toma un valor menor que en sus alrededores. \[\text{Si } f'(x_0) = 0 \quad \Rightarrow \quad \text{posible máximo o mínimo en } x_0.\] \[\textbf{Ejemplo: } f(x) = x^2\] \[f'(x) = 2x \quad \Rightarrow \quad f'(0)=0\] \[f''(x) = 2 > 0 \quad \Rightarrow \quad \text{mínimo relativo en } x=0.\]--- Criterio de la segunda derivada: \[f''(x_0) > 0 \;\; \Rightarrow \;\; \text{mínimo relativo en } x_0\] \[f''(x_0) < 0 \;\; \Rightarrow \;\; \text{máximo relativo en } x_0\] \[f''(x_0) = 0 \;\; \Rightarrow \;\; \text{indeterminado (se revisa más con derivadas superiores).}\]--- Criterio de la tercera derivada (generalización): Si se cumple que \[f'(x_0) = f''(x_0) = \dots = f^{(n-1)}(x_0) = 0, \quad f^{(n)}(x_0) \neq 0\] - Si \(n\) es par y \(f^{(n)}(x_0) > 0 \;\;\Rightarrow\;\; \text{mínimo relativo.}\) - Si \(n\) es par y \(f^{(n)}(x_0) < 0 \;\;\Rightarrow\;\; \text{máximo relativo.}\) - Si \(n\) es impar \(\;\Rightarrow\;\) no hay máximo ni mínimo, sino punto de inflexión.

El \(\text{Teorema Fundamental del Cálculo}\) establece la conexión entre derivadas e integrales: La integral definida de una función continua es igual a la diferencia de los valores de su primitiva en los extremos.
\[\int_a^b f(x)\,dx = F(b) - F(a)\]
donde \(F(x)\) es una función tal que \(F'(x) = f(x)\). De esta manera, el cálculo integral y el diferencial quedan unidos en un mismo marco matemático.

La \(\text{integral}\) se entiende como la \(\text{inversa de la derivada}\). \[f(x) = x^2 \quad \Rightarrow \quad f'(x) = 2x\] Entonces, integrar devuelve la función original (más una constante): \[\int 2x \, dx = x^2 + C\] --- Otra interpretación de la integral es el \(\text{área bajo la curva}\) entre \(a\) y \(b\). Se aproxima dividiendo el intervalo en muchos rectángulos: \[\sum_{i=1}^{n} f(x_i) \cdot \Delta x\] Al tomar cada vez más rectángulos (\(\Delta x \to 0\), \(n \to \infty\)) se obtiene la definición formal de la integral definida: \[\int_a^b f(x)\,dx = \lim_{n \to \infty} \sum_{i=1}^{n} f(x_i)\,\Delta x\]

La regla de la cadena en integrales se usa cuando tenemos una función compuesta del tipo \( f(g(x)) \cdot g'(x) \). En ese caso: \[\int f(g(x)) \, g'(x) \, dx = F(g(x)) + C\] donde \(F\) es una primitiva de \(f\). Ejemplo: \[\int 2x \cos(x^2) \, dx\] Hacemos el cambio \( u = x^2 \), entonces \( du = 2x \, dx \). La integral se convierte en: \[\int \cos(u) \, du = \sin(u) + C\] Reemplazamos \( u = x^2 \): \[\int 2x \cos(x^2) \, dx = \sin(x^2) + C\]

La sumatoria de Riemann es un método para aproximar el área bajo una curva. Se divide el intervalo \([a,b]\) en \(n\) subintervalos de ancho \(\Delta x = \frac{b-a}{n}\). En cada subintervalo se toma un punto \(x_i^*\) y se evalúa la función \(f(x)\). La suma de las áreas de los rectángulos formados es: \[S_n = \sum_{i=1}^{n} f(x_i^*) \, \Delta x\] Cuando el número de particiones \(n\) crece indefinidamente, los rectángulos se vuelven más delgados y la suma se aproxima al área exacta bajo la curva. El límite de estas sumas es lo que definimos como la integral definida: \[\int_a^b f(x) \, dx = \lim_{n \to \infty} \sum_{i=1}^{n} f(x_i^*) \, \Delta x\] De esta manera, la integral representa el área exacta bajo la gráfica de \(f(x)\) entre \(x=a\) y \(x=b\).

A donde sea que mire, Todo me lleva a Jesus

PADRE - CALCULO DIFERENCIAL

HIJO - CALCULO INTEGRAL

ESPIRITU SANTO - CALCULO MULTIVARIABLE/VECTORIAL